Depth First Search Algorithm(DFS)
그래프를 탐색하는 방법중 대표적인 DFS, BFS 중 DFS 알고리즘에 대해서 알아보려고 한다.
알고리즘 문제를 접할때 솔루션으로 많이 접하는 알고리즘이기도 하고 해당 탐색으로 부터 해서 특정 조건이 추가 됨으로써 백트래킹으로 확장(?)되기도 하며 최단거리 혹은 경로를 구하는 문제로 적용(확장) 되기도 합니다.
어찌되었든, 그래프를 탐색하는 방법인 Depth First Search Alogithm에 대해서 알아보도록 하겠습니다.
정의(Definition)
그래프 탐색의 한종류로, 특정노드로부터 시작하여 최대로 진입하
'깊이 우선 탐색' 이름에서 알 수 있는 것처럼, 가능한 그래프상에서 '더 깊이', '더 깊게' 탐색을 진행하는 그래프 탐색 방법이다.
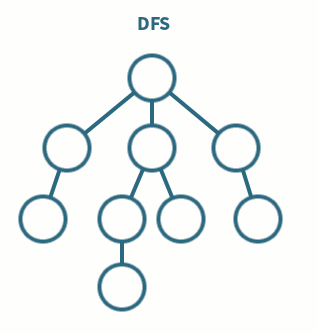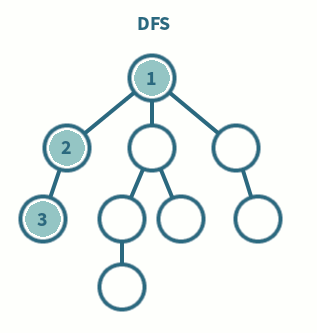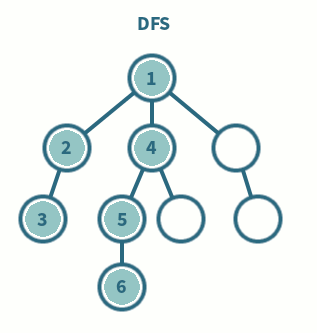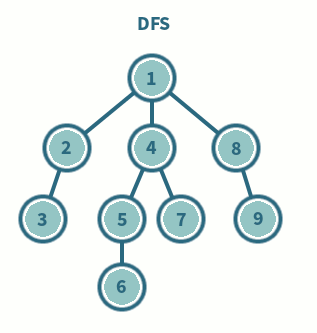
여기서 그래프는 자료구조 중 하나로 여러 종류가 있지만 우선 정점(vertex)와 두 정점을 연결하는 간선(Edge)의 집합이라고 이해하면 될듯하다.(추후 따로 정리하도록함)
깊이 우선 탐색은 가장 최근에 발견하고 아직 찾지않은 간선을 갖는 vertex로부터 나오는 간선을 조회

우선 A부터 진행되니 A를
어떻게 진행될까?
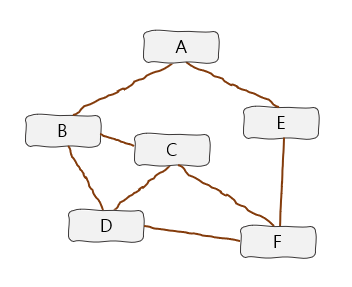
우선 다음과 같은 그래프가 주어졌을때...A를 시작점으로 DFS를 진행한다고 가정해보겠다.
- 탐색한 vertex를 방문(visited) 처리한다.
- 해당 vertex와 인접한 모든 vertex중 방문하지 않은 vertex를 방문한다
우선 기본진행은 간단하다.
하지만, 여기서 고려할게 있는데 우선 인접한 모든 vertex를 보관하고 있어야한다는 거다.
그리고 이미 방문(visited) 처리가 되었는지 확인하고 이미 처리가 되었다면 더이상 방문하지 않는 것인데 이 부분은 Stack 으로 처리할 수 있다.
좀 더 진행을 자세히 살펴 보도록 하겠다.
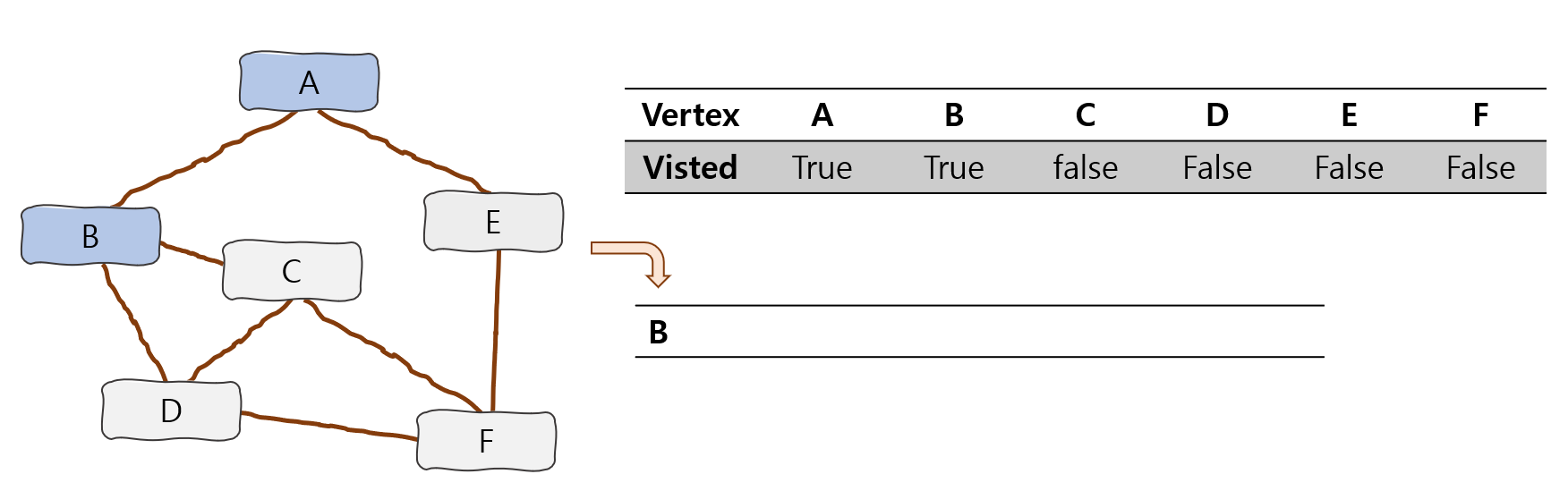
우선 A에서 시작이므로 A는 visted 처리를 해주도록 하겠다.(시작점임 A의 경우에도 구현방식에 따라 다르겠지만, Stack에 들어가 있다고 볼 수 있다.)
그 후 A에서 방문할수 있는 인접 정점인 B, E 중 알파벳 순서상 B를 우선으로 방문처리후 Stack에 넣어준다.
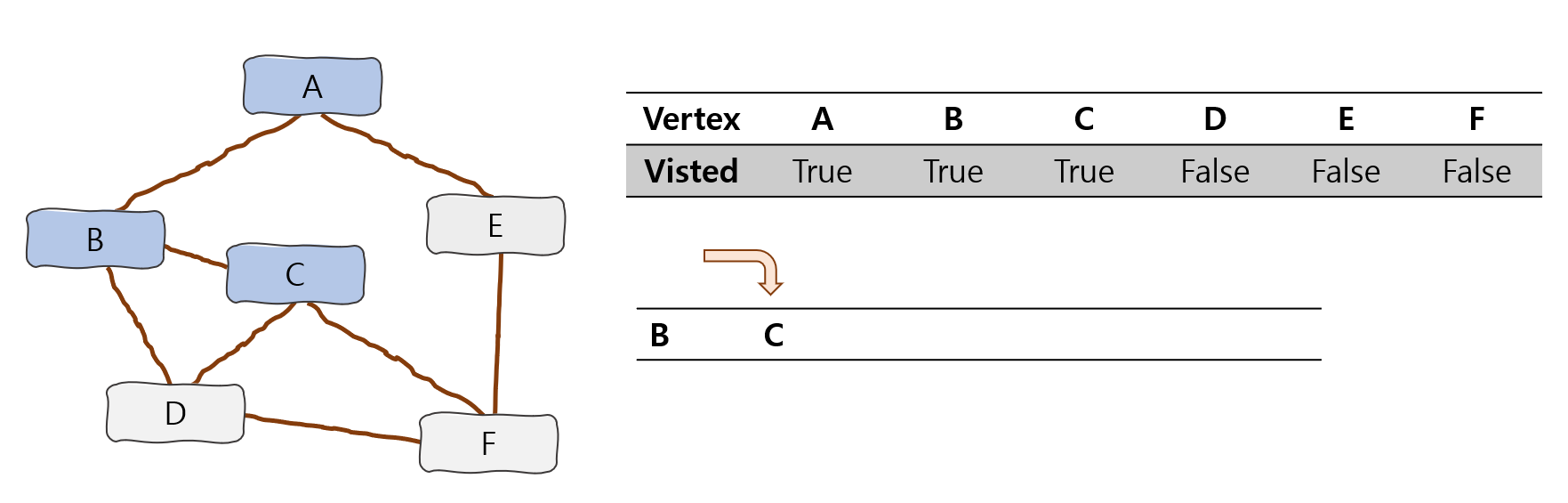
위 과정과 똑같이 C 정점은 방문 여부 확인후 미방문시 방문처리후 Stack에 넣어준다.
이러한 과정을 반복하면 다음과 같은 진행이 될 것이다.
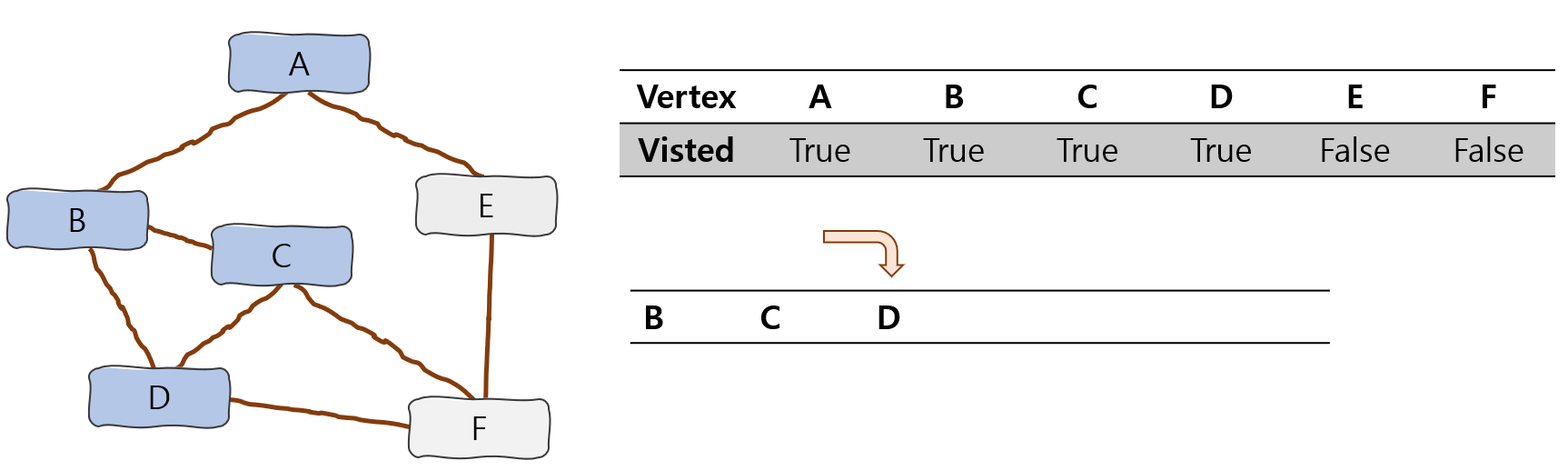
해당그래프는 아마 전부 이어져 있기 때문에 F, E 정점을 순서대로 Push 해주게 될 것이다.
그리고 더이상 인접한 정점에서 방문할 수 있는 vertex 가 없다면 pop 해주면 된다.
소스코드
/*
기본적으로 행렬기반으로 구현
v : vertex
e : edge
n : vertex의 개수
m : edge의 개수
Edge_table : 간선 연결 여부 테이블
Vertex_table : 정점 visit 여부 확인 테이블
Finish_table : 탐색이 완료된 정점 순서대로 저장하는 테이블
Visit_table : visit 된 순서대로 vertex를 저장
UN_VISIT : 아직 탐색
VISIT : 자식 탐색이 종료
*/
#define MAX_VERTEX 101
#define VISIT 1
#define UN_VISIT 0
#define CONNECTED 1
int Edge_table[MAX_VERTEX][MAX_VERTEX];
int Vertex_table[MAX_VERTEX];
void DFS(int v_i) {
Vertex_table[v_i] = VISIT;
cout << v_i << " ";
for (int i = 0; i < MAX_VERTEX; i++) {
if (Edge_table[v_i][i] == CONNECTED && Vertex_table[i] == UN_VISIT) {
DFS(i);
}
}
}해당 소스코드는 각 정점의 연결여부... 즉, 그래프를 행렬로 표현한 코드를 이용한다.
그래프의 표현은 인접행렬로도 인접리스트로도 할 수 있기 때문에 그에 따른 코드 구현에 따라 코드의 내용은 조금 달라질 수 있으나, 행렬과 리스트의 차이점을 통해 적절한 코드를 이용하면 될 듯하다.
시간복잡도
위에서 말한거와 같이 행렬이냐 리스트냐에 따라서 시간복잡도가 조금 달라진다.(행렬과 리스트의 차이)
우선 행렬로 그래프를 표현했을때의 시간복잡도는 다음과 같다.
$$O(N^2)$$
다만, 리스트로 작성했을때는 다음과 같다.
$$O(N+e)$$
여기서 N의 값은 vertex. 즉, 정점의 갯수를 의미한다.
참고서적
- Introduction to Algorithm - DFS
'공부방 > 알고리즘' 카테고리의 다른 글
| Longest Common Sub-sequence Algorithm(LCS, 최장 공통 부분수열) (0) | 2021.12.21 |
|---|---|
| Longest Increasing Sub-sequence Algorithm(LIS, 최장 증가 부분 수열 알고리즘) (0) | 2021.12.14 |
| Binary Search Algorithm(이진 탐색 알고리즘) (0) | 2021.11.18 |
| Recursion Algorithm(재귀 알고리즘) (0) | 2021.10.15 |
| Euclidean algorithm(유클리드 호제법) (0) | 2021.07.20 |
