Recursion Algorithm

처음 재귀를 접하게 되면 이해가 안될 것이다. 다만 위 그림을 보면 대충 재귀가 무엇인지 감이 잡힐 것이다.
재귀에 대해서 알아보면 임의의 함수가 자기자신을 호출하는 재귀 호출을 이용하는 알고리즘이다.
같은 행동을 반복적으로 행할때 사용하는 알고리즘인 것이다. 그렇다면 재귀알고리즘은 반복문과는 어떠한 차이가 있을까? 그리고 재귀를 이용함으로써 얻을수 있는 이점은 무엇이고 단점은 무엇인가를 알아보고자한다.
정의(Definition)
임의의 함수가 자기자신을 호출하는 것으로 그 함수를 재귀함수라하며 그 호출을 재귀호출이라한다.
이렇듯 재귀알고리즘은 스스로를 호출하는 함수를 이용한 풀이를 재귀 알고리즘이라고 말한다.
재귀알고리즘을 이용하기 위해 재귀함수를 만들때는 중요한 점들이 있다.
- 언제 재귀를 멈출 것인가? 탈출할 것인가? 즉, 탈출조건
- 재귀를 발생시키는 지점을 어떻게 정할 것인가? 즉, 어느 분기에서 재귀호출을 수행하는가?
- return 값을 제대로 정의하는가?
개인적으로 재귀를 만들때 중요한것은 이렇게 3가지 인거 같다.
재귀를 왜 쓸까?
그렇다면 재귀는 왜 쓸까? 재귀를 쓰면서 얻을수 있는 이점이 무엇이 있을까?
- 가독성
- 변수의 사용
둘 다 비슷한 말인거 같다. 물론 1번에서 말하는 가독성은 논리적 흐름이 재귀적으로 표현하는 것이 자연스러울 경우 짧으면서도 더욱 직관적으로 전체를 이해할수 있는 경우가 있다.
예를 들어 팰토리얼 함수를 예를 들어보겠다.
int factorial(int n)
int result = 1;
for(int i = 1; i <= n; i++)
result *= i;
return result;
}반복문으로 작성한 코드이다. 물론 문제가 간단한만큼 이해도 쉽지만 이것을 재귀함수로 바꾸면 다음과 같다.
int recursive_factorial(int n)
if(n==1) return 1;
return n * recursive_factorial(n-1);
}여기서 보다시피 논리적으로 n!을 구하기 위해서는 n값과 n-1!값의 곱셈임을 알 수가 있다. 그리고 여기서 result라는 변수도 사용하지 않고 있다. 이렇듯 코드가 간결해지고 보기에 편해지는 장점이 있다.
하지만 재귀를 사용할때는 많은 것을 조심해야한다. 기본적으로 탈출 조건을 잘 명시해야겠지만 그외에도 보이지 않게 메모리적 측면, 속도 측면에서의 성능관련 이슈가 발생하게 된다.
이러한 점을 주의하고 관리하면서 재귀를 사용할 수 있어야 할 것같다.
콜 스택(Call Stack)
재귀가 진행되는 동안 프로그램 내부에서는 어떠한 일이 일어나는지 살표 볼 필요가 있다.
우선 재귀의 호출은 stack의 구조로 이루어져 있으며 프로그램이 함수를 호출을 추적할때 사용된다.
일반적으로 call stack은 함수호출 하나당 하나의 스택블록으로 이루어진다.
int countdown(int num) {
if(num == 1) {
return num;
}
return countdown(num - 1);
}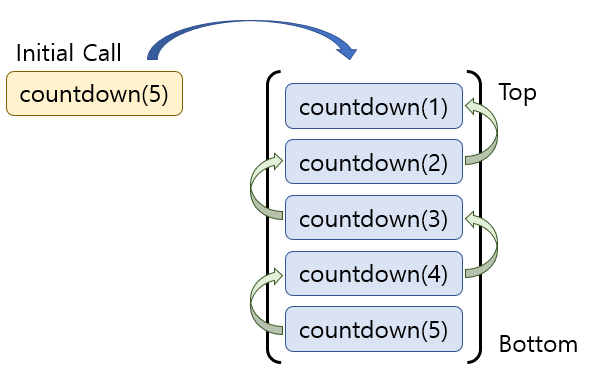
코드상에서 초기 num값이 5로 설정된다면 countdown(5)가 호출되면 countdown은 먼저 스택에 쌓이고 countdown(4)를 호출하게된다. 그리고 똑같은 과정을 지나서 countdown(3)을 호출하게 되고 countdown(1)이 호출 될때까지 반복하게 된다.
countdown(1)이 호출되면 num의 값이 1로 탈출조건을 만족하며 재귀가 멈추게 된다. 그렇게 탈출을 하게 되면 그때 stack에서 countdown(1)이 리턴되면서 삭제된다 그리고 countdown(1)를 호출한 countdown(2)를 찾게되고 그 결과가 리턴되면서 stack에서 삭제된다.
즉, 재귀는 호출하며 호출한 함수가 리턴되어올때까지 메모리상에 올려져 있게 된다. 이는 재귀가 호출이 많으면 많아질수록 재귀의 깊이가 깊어질수록 메모리에 쌓이는 양이 많아지게 되고 거기서 크리티컬한 문제들이 발생된다.
오버플로우(Overflow)
재귀의 Call Stack을 확인하면 알 수 있는 것 처럼 재귀는 스스로를 호출하면서 계속해서 Stack에 함수호출을 쌓아간다.
이 경우 적절한 탈출조건을 만들지 못하면 재귀가 탈출하지 못하고 계속 끊임없이 stack메모리 영역을 차지 하게 된다.
그러다 정해진 stack 메모리를 넘어서 heap 메모리 영역을 침범하게 되면 overflow문제가 발생할 수 있는 위험이 있다.
그렇기 때문에 재귀를 사용하게 될 경우에는 최대 깊이(maximum depth)를 정해서 예외처리를 하기도한다.
속도(Speed)
재귀는 위에서 말한거와 같이 동일한 함수를 지속적으로 만들게 되면서 함수를 만드는데 필요한 메모리를 계속해서 생성하게 된다. 이렇게 함수의 매개변수, 지역변수, 리턴값 그리고 함수가 종료된후 돌아가는 위치를 스택에 저장하고 반환하면서 많은 context switching 비용이 발생하게 되므로 그로인한 속도가 사실상 반복문보다 느립니다.
꼬리재귀(Tail Recursion)
Tail Call Optimization을 재귀에 적용한 것으로 Tail Call로 자기 자신을 호출하는 함수이다.
기존 재귀함수는 함수호출시 함수의 매개변수, 지역변수, 리턴값 그리고 함수가 종료된후 돌아가는 위치를 스택 메모리에 저장하기에 많이 느리게 되는데 그 해결책중 하나의 방법으로 Tail Call Optimization을 이용한 꼬리재귀(Tail Recursion)이 있습니다.
Tail Call Optimization
Tail Call 방식으로 코드가 작성될 경우 stack block을 새로 만들지 않고 이미 있는 stack 속의 값만 대체하여 stack을 재사용하게 되어 동작을 최적화 할 수 있다.
주의..!! 이것은 각 언어의 실행환경에서 지원을 해주어야 사용할 수 있어 각 실행환경이 해당 최적화를 적용할 수 있는지 확인이 필요하다.
Example
int recursive(int n){
if(n==1)
return 1;
return n + recursive(n-1);
}기존의 재귀함수를 보면 n+recursive(n-1)의 연산을 필요로 하게 된다.
int tail_recursive(int n, int acc){
if(n==1)
return acc;
return tail_recursive(n-1, n + acc);
}꼬리 재귀함수로 짜여진 코드를 보면 return에 연산을 기다리고 있지 않다.
또한 이러한 재귀의 방식을 도와주기 위해 메모이제이션(Memoization)이 사용되기도 한다. 메모이제이션에 대해서는 나중에 동적계획법을 정리하면서 따로 정리하도록 하겠습니다.
'공부방 > 알고리즘' 카테고리의 다른 글
| Longest Increasing Sub-sequence Algorithm(LIS, 최장 증가 부분 수열 알고리즘) (0) | 2021.12.14 |
|---|---|
| Binary Search Algorithm(이진 탐색 알고리즘) (0) | 2021.11.18 |
| Euclidean algorithm(유클리드 호제법) (0) | 2021.07.20 |
| Sieve of Eratosthenes(에라토스테네스의 체) (0) | 2021.07.20 |
| Hanoi Tower(하노이의 탑) (0) | 2021.07.19 |
