Longest Common Sub-sequence Algorithm(LCS)
LIS알고리즘을 정리하다가 비슷한류의 알고리즘으로 보여 함께 이어서 정리하려고 한다.
이문제 또한 아마 DP를 이용한 문제가 될것으로 생각된다. 다만 문자로 이루어진 수열이기에 LIS에서 사용했던 이분탐색은 불가능해보인다.
그리고 해당 문제에서도 길이 뿐만이 아닌 해당 부분수열을 구하는 방법도 알아보도록 하겠다.
정의(Definition)
최장 공통 부분수열으로 두 문자열의 가장 긴 공통된 부분문자열을 구하는 문제
Longest Common Sub-sequence 불린다. 여기서 string이 아닌 sequence는 사용하는 이유는 각 단어가 갖는 개념적 의미가 다르기 때문이다.
- string : 연속된 문자열
- sequence : 연속되지 않는 수열
즉, 부분 문자열을 구하는 문제로 sub-sequnce를 사용하며 명칭은 longest common sub-sequence가 된다.

명칭과 위 그림에서도 알 수 있다시피 2개의 문자열이 주어졌을때, 공통 부분 문자열중 가장 긴 부분 문자열을 구하는 문제가 될 것이다. 그리고, 해당 문제도 LIS와 비슷하게 해결하는 목적에 따라 또 조금씩 접근 방법이 달라진다
- LCS 길이구하기
- LCS 구하기
LCS 길이구하기
LCS의 길이를 구하게 될때는 결국 DP(Dynamic Programming)을 사용하게 될 것이다.
우선 점화식을 파악하기 위해서 일단 진행이 어떻게 되는지 살펴보도록 하겠다.
LCS의 진행
두 문자열 'GCABCD' 그리고 'ABDCED'가 주어졌을 때, LCS를 구하는 진행과정은 다음과 같다.
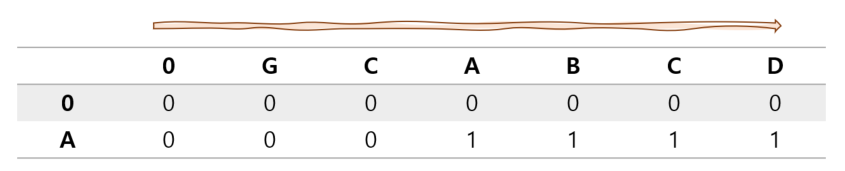
위 그림에서 보다시피 {GCA}, {GCAB}, {GCABC}, {GCABCD}와 {A}를 비교하면 공통 수열이 1임을 알수 있다.

{ABDCED} 문자열의 B를 추가하여 비교를 해보면 위 그림과 같다. {GCA}, {GCAB}, {GCABC}, {GCABCD}와 {AB}를 비교하게 되기 때문에 {GCABCD} 문자열의 A 이후 B와 일치하는 부분을 보면 {GCAB}, {GCABC}, {GCABCD} 와의 길이가 2가 됨을 알 수 있다.
이어서 진행되는 과정들을 쭉 보면 다음과 같이 진행될 것이다.

이렇게 진행을 따라가다보면 다음과 같은 규칙들을 따라감을 알 수 있다.
LCS 길이 진행 규칙(점화식)
- 문자열의 비교가 같은 경우 : 부분 문자열 증가. 즉, 대각선 왼쪽 위까지의 진행상 길이 + 1
- 문자열의 비교가 다른 경우 : 현재 진행상황의 왼쪽과 위쪽 값중 더 큰 값
즉 점화식은 다음과 같게 된다.
$$ LCS(X_i, Y_j) = \begin{cases} 0 & \mbox{if } i=0 \mbox{ or } j=0 \\ LCS(X_{i-1}, Y_{j-1}) & \mbox{if } X_i = Y_j \\ Longest(LCS(X_i, Y_{j-1}), LCS(X_{i-1}, Y_j)) & \mbox{if } X_i \ne Y_j \end{cases}$$
소스코드
int longest(int num1, num2) {
return num1 > num2 ? num1 : num2;
}
int lcs_dp(string str1, string str2) {
int max_length = 0;
for(int j = 0; j < str2.length; j++) {
for(int i = 0; i < str1.length; i++) {
if(i == 0 || j == 0) lcs[i][j] = 0;
else if(str1[i-1] == str2[j-1]) lcs[i][j] = lcs[i-1][j-1] + 1;
else lcs[i][j] = longest(lcs[i-1][j], lcs[i][j-1]);
max_length = max_length > lcs[i][j] ? max_length : lcs[i][j];
}
}
return max_length;
}
시간복잡도
소스코드나 해당 진행과정을 살펴봐도 두 문자열을 2중탐색을 진행하는 것을 알 수있다.
즉, 문자열의 길이를 N이라고 한다면 시간복잡도는 다음과 같다.
$$O(N^2)$$
LCS 구하기
지금까지 LCS의 길이를 구했다면, LCS자체는 어떻게 구할 수 있을까?
LIS에서의 경우를 생각해보면 길이를 통해 구하던 것을 알 수가있다.

위 그림과 같이 가장긴 길이 4부터 시작하여 3, 2, 1이 나타나는 첫지점의 값을 찾아서 해당위치의 문자를 찾아서 나열하면 된다.
즉 찾는 순서대로 stack에 넣은후 순서대로 stack에서 뺀다면 해당문자열을 구할 수 있는 것이다.
소스코드
void print_lcs(string str1, string str2) {
int i = str1.length - 1;
int j = str2.length - 1;
stack<char> st;
while(lcs[i][j] != 0) {
if(lcs[i][j] == lcs[i][j-1]) j--;
else if(lcs[i][j] = lcs[i-1][j]) i--;
else {
st.push(str1[i]);
i--;
j--;
}
}
while(!st.empty()) {
cout << st.top();
st.pop();
}
}[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence
LCS는 주로 최장 공통 부분수열(Longest Common Subsequence)을 말합니다만, 최장 공통 문자열(Longest Common Substring)을 말하기도 합니다.
velog.io
알고리즘 - LCS(Longest Common Subsequence, 최장 공통 부분 문자열) 알고리즘
LCS 알고리즘이란?
chanhuiseok.github.io
LCS(Longest Common Subsequence) 알고리즘
1. 개요 LCS란 Longest Common Subsequence의 약자로 최장 공통 부분 문자열이다. 우리가 알고 있는 substring과 비교하면 substring은 연속된 부분 문자열이고 subsequence는 연속적이지는 않은 부분 문자열..
twinw.tistory.com
'공부방 > 알고리즘' 카테고리의 다른 글
| Depth First Search Algorithm(DFS, 깊이 우선 탐색) (0) | 2022.01.05 |
|---|---|
| Longest Increasing Sub-sequence Algorithm(LIS, 최장 증가 부분 수열 알고리즘) (0) | 2021.12.14 |
| Binary Search Algorithm(이진 탐색 알고리즘) (0) | 2021.11.18 |
| Recursion Algorithm(재귀 알고리즘) (0) | 2021.10.15 |
| Euclidean algorithm(유클리드 호제법) (0) | 2021.07.20 |
