문제
1010번: 다리 놓기
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
www.acmicpc.net
문제파악
문제를 읽어보면 강을 중심으로 왼쪽 영역 N개에서 오른쪽 영역 M개의 영역으로 다리를 연결하게 되는데 그 때 가능한 케이스의 갯수를 구하는 문제이다.
이경우 다음과 같이 한영역에 다리가 겹쳐지거다 교차될 수 없다고 한다. 다음 그림을 보면 좀더 이해가 쉬울 거 같다.
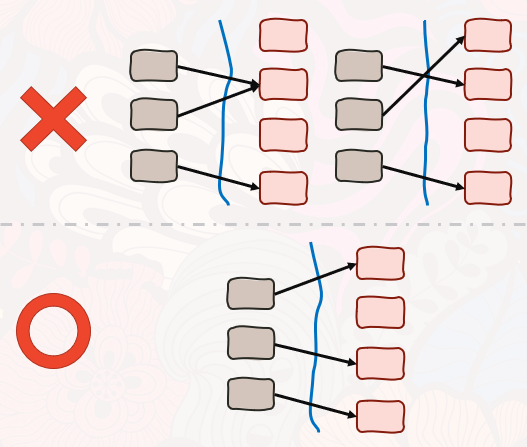
이렇게 봤을 때...문제를 어떻게 해결할 수 있을까 생각해보면, M영역 즉, 우측지역의 영역에서 N(좌측)영역의 지역의 갯수만큼 선택해서 순서대로 연결해주면 교차하지도 않고 겹치지도 않게 구할 수 있는 문제가 된다.
즉, 우측영역 M개에서 좌측 영역 N개를 먼저 선택을 하면 되는 문제로 보인다.
그렇게 생각할때 문제를 해결할 수 있는 방법을 떠올려보면, 조합을 이용해서 문제를 해결 할 수 있다.
문제풀이
문제 파악을 통해 해당 문제를 조합을 통해 문제를 해결 할 수 있음을 확인했다.
$$_{n}\mathrm{C}_{r}={n \choose r}={n!\over r!(n-r)!}$$
조합에 대한 식을 확인해보면 떠오르는게 없을 수 있지만 그 성질을 보면 확 떠오르는게 있다.
$$_{n}\mathrm{C}_{r} = _{n-1}\mathrm{C}_{r-1} + _{n-1}\mathrm{C}_{r} \quad and\quad _{n}\mathrm{C}_{0}=_{n}\mathrm{C}_{n}=1$$
조합은 위 성질을 만족하는데 해당 성질이 하나의 점화식 기준을 만족시키게 된다. 그리고 그결과 dp를 이용하면 쉽게 구현할 수 있는 문제가 되어버린것이다.
해당 문제 또한 재귀 혹은 반복문을 통해 구현할 수 있고 메모이제이션을 이용하면 속도측면에서 문제를 해결하는데 도음이 될 수 있다.
Solution 1(반복문)
#include<iostream>
using namespace std;
int main() {
int combi_arr[30][30];
for (int n = 1;n < 30;n++) {
for (int r = 0; r <= n; r++) {
if (n == r || r == 0) {
combi_arr[n][r] = 1;
}
else {
combi_arr[n][r] = combi_arr[n - 1][r - 1] + combi_arr[n - 1][r];
}
}
}
int t;
cin >> t;
while (t--)
{
int n, m;
cin >> n >> m;
cout << combi_arr[m][n] << endl;
}
return 0;
}'문제풀이' 카테고리의 다른 글
| BaekJoon(9012)::괄호 (0) | 2021.12.02 |
|---|---|
| BaekJoon(1003)::피보나치 함수 (0) | 2021.11.24 |
| BaekJoon(9461)::파도반 수열 (0) | 2021.11.22 |
| LeetCode(977)::Squares of a Sorted Array (0) | 2021.11.18 |
| LeetCode(344)::Reverse String (0) | 2021.11.18 |
