문제
9461번: 파도반 수열
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의
www.acmicpc.net
문제파악
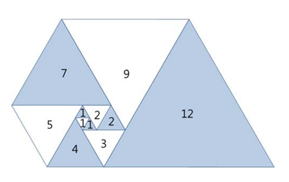
파도반 수열은 리처드 파도반에 의해 이름이 붙여졌으며, 오른쪽 그림과 같이 삼각형들이 한변의 길이를 공유한 상태로 나선형으로 계속해서 이어지는 삼각형이다.
해당 수열이 진행을 보면 다음과 같다
1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37
수열과 같은 문제를 풀다보면 대부분 점화식을 찾아내면 쉽게 해결할 수 있다.
파도반 수열의 점화식은 다음과 같다
$$f(n)=\begin{cases}1 & \mbox{if }n=\mbox{ 0,1,2} \\f(n-2)+f(n-3), & \mbox{if }3 \leqq\mbox{ n}\end{cases}$$
문제풀이
위 점화식을 피보나치 수열과 같이 재귀를 통하거나 반복문을 통해 구현을 해두거나, 미리 n 최대 사이즈까지 수열을 전부 저장해서 갖고 있으면 된다.
#include<iostream>
using namespace std;
int main() {
unsigned long padovan_arr[101];
padovan_arr[0] = 0;
padovan_arr[1] = padovan_arr[2] = 1;
for (int i = 3; i < 101;i++) {
padovan_arr[i] = padovan_arr[i - 3] + padovan_arr[i - 2];
}
int t_case;
cin >> t_case;
while (t_case--) {
int n;
cin >> n;
cout << padovan_arr[n] << endl;
}
return 0;
}헌데 문제를 진행해보면 점화식을 다음과 같이 구성해도 된다. 다만, 저경우 n이 4까지는 값을 구해두어야한다.
$$f(n-3)+f(n-2) \rightarrow f(n-5)+f(n-1)$$
'문제풀이' 카테고리의 다른 글
| BaekJoon(1003)::피보나치 함수 (0) | 2021.11.24 |
|---|---|
| BaekJoon(1010)::다리놓기 (0) | 2021.11.23 |
| LeetCode(977)::Squares of a Sorted Array (0) | 2021.11.18 |
| LeetCode(344)::Reverse String (0) | 2021.11.18 |
| LeetCode(344)::Reverse String (0) | 2021.11.18 |
