Hanoi Tower(하노이의 탑)
프랑스 수학자 에두아르 뤼카가 클라우드 교수라는 필명으로 발표하였고 그 후 1년 후 헨리 드 파르빌이 다음과 같은 이야기로 하노이 탑을 소개하였다.
인도베나레스에 있는 한 사원에는 세상의 중심을 나타내는 큰 돔이 있고 그 안에 세 개의 다이아몬드 바늘이 동판 위에 세워져 있습니다. 바늘의 높이는 1 큐빗이고 굵기는 벌의 몸통만 합니다.
바늘 가운데 하나에는 신이 64개의 순금 원판을 끼워 놓았습니다. 가장 큰 원판이 바닥에 놓여 있고, 나머지 원판들이 점점 작아지며 꼭대기까지 쌓아 있습니다. 이것은 신성한 브라흐마의 탑입니다.
브라흐마의 지시에 따라 승려들은 모든 원판을 다른 바늘로 옮기기 위해 밤낮 없이 차례로 제단에 올라 규칙에 따라 원판을 하나씩 옮깁니다.
이 일이 끝날 때, 탑은 무너지고 세상은 종말을 맞이하게 됩니다.
문제 소개
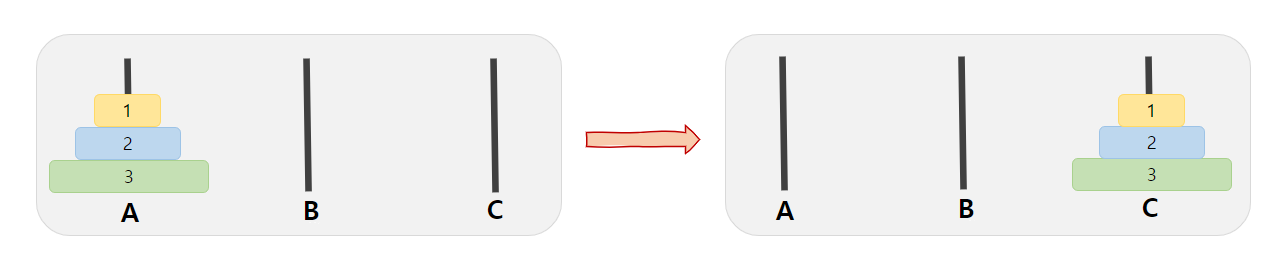
위의 그림과 같이 3개의 기둥에서 첫번째 기둥에 있는 원반을 모두 세번째 위치에 있는 기둥으로 옮기는 문제가 된다.
다만 해당 원반의 크기는 전부 다르고 원반을 옮기는 것에 있어서 다음 조건을 만족하면 원반을 이동해야한다.
- 한 번에 하나의 원반만을 움직일 수 있다.
- 원반은 오직 자기보다 큰 원반 위에 놓을 수 있다.(즉, 위로 가면서 더 작은 원반을 쌓아야한다.)
위 조건을 만족하며 옮기는 것이 기본적인 하노이 탑의 목표가 된다.
'A'기둥에 놓여진 원반을 조건을 만족(순서를 지키며) 최종적으로 'C' 기둥으로 옮기는 것이다.
문제 정의
하노이 탑은 크게 두개의 문제로 나뉘어 질 수 있다.
- 최소 이동 횟수
- 원반의 이동 순서
다음과 같은 문제로 표현할 수 있으며 위 문제를 정의하면 다음과 같다.
원반의 개수(n)가 주어졌을 때, 최소 이동 횟수 혹은, 원반의 이동 순서를 출력한다.
input : 원반의 총 갯수 n
output : 최소 이동 횟수 or 원반의 이동 순서
문제 풀이

다음 그림을 보면 3개의 원판을 옮길때를 자세히 살펴보면 2개의 원판을 옮기고 3번째 원판을 옮기는 것을 볼 수 있다.
- 2개의 원판을 B로 옮긴다.
- 3번째원판(하나남은 원판을 C로 옮긴다)
- 2개의 원판을 다시 C로 옮긴다.
이렇게 3개의 Step으로 나눌 수 있음을 볼 수 있다.
즉, n개의 원판을 옮길대 n-1개의 원판을 옮기는 과정을 통해 문제를 해결 할 수 있으며, 작은 문제를 풀어 해결하는 과정을 통해 재귀를 이용할 수 있다.
재귀
재귀로 해당 문제를 표현하기 위해 위 정리를 살펴보면 다음과 같이 내용을 바꿀 수 있다.
'hanoi(N)을 수행한다고 가정해보자'
- hanoi(N-1) 수행
- N번 째 원판을 C로 옮긴다.
- hanoi(N-1) 수행
그렇다면 위 단계와 3개의 기둥과 hanoi(n)의 관계를 생각해보면 출발, 경유, 도착의 개념으로 나누어 생각 할 수 있다.
- hanoi(N-1)을 A에서 출발하여 C를 경유해 B로 이동
- N번째 원판을 C로 이동
- hanoi(N-1)를 B에서 A를 경유하여 C로 이동
출발, 경유, 도착의 개념을 통해 재귀의 표현을 좀 더 명확히 할 수 있다.
그러면 이제 위 표현을 통해 수식으로 표현해 보자.
$$hanoi(N, start, to, via)= \begin{cases}move(1, start, to) \\ hanoi(N-1, start, via, to) + move(N, start, to) + hanoi(N-1, via, start, to) \end{cases}$$
위 표현은 다음 수식으로 표현할 수 있고 n이 1인 경우가 탈출 조건이 된다.
그럼 이경우를 소스코드로 표현해 보면 다음과 같다.
void move(N, from, to) {
cout << "N : " << from << " -> " << to <<endl;
return;
}
void hanoi(N, from, via, to) {
if(N == 1) {
move(1, from, to);
return;
}
hanoi(N-1, from, to, via);
move(N-1, from, to);
hanoi(N-1, via, from, to);
return;
}
이동 횟수
해당 이동 횟수를 문제로 정의시 해당 문제는 먼저 재귀식을 구한 후 해당재귀식의 일반항을 도출하여 해결할 수 있다.
먼저 재귀식을 구하기 위해 위 재귀표현을 보면 hanoi(N-1)이 2번 수행후 move가 1번 수행됩니다.
$$hanoi(N)= \begin{cases}1 & \mbox{ if N}\mbox{ == 1} \\ 2 \times hanoi(N-1) + 1 & \mbox{ else} \end{cases}$$
해당 재귀식을 통해 일반 항을 도출할 수 있는데 다음 과정을 통해 도출된다.
$$ hanoi_n = hanoi_{n-1} \times 2 + 1$$
위 식의 양변에 1을 더하면 다음과 같은 식의 진행을 볼 수 있다.
$$ hanoi_n + 1 = 2 \times (hanoi_{n-1} + 1)$$
$$ hanoi_{n-1} + 1 = 2 \times (hanoi_{n-2} + 1)$$
$$ hanoi_{n-2} + 1 = 2 \times (hanoi_{n-3} + 1)$$
$$ \vdots $$
$$ hanoi_2 + 1 = 2 \times (hanoi_1 + 1)$$
이때 각 좌변과 우변을 곱하면 다음 식을 구할 수 있다.
$$ (hanoi_n+1)(hanoi_{n-1}+1) \cdots (hanoi_2+1) =2^{n-1} (hanoi_{n-1}+1)(hanoi_{n-2}+1) \cdots (hanoi_1 + 1)$$
그리고 공통된 인자로 나누어준다.
$$ (hanoi_n+1) = 2^{n-1} \times (hanoi_1+1) $$
여기서 $hanoi_1$은 1이기 때문에 하노이 탑의 일반항은 다음과 같다.
$$ (hanoi_n) = 2^{n-1} - 1 $$
해당 일반항을 통해 굳이 move 함수를 count하지 않더라도 N의 값을 통해 총 이동 횟수를 바로 구해 낼 수 있다.
'공부방 > 알고리즘' 카테고리의 다른 글
| Longest Increasing Sub-sequence Algorithm(LIS, 최장 증가 부분 수열 알고리즘) (0) | 2021.12.14 |
|---|---|
| Binary Search Algorithm(이진 탐색 알고리즘) (0) | 2021.11.18 |
| Recursion Algorithm(재귀 알고리즘) (0) | 2021.10.15 |
| Euclidean algorithm(유클리드 호제법) (0) | 2021.07.20 |
| Sieve of Eratosthenes(에라토스테네스의 체) (0) | 2021.07.20 |
